

However, in a hyperbola, the two arms or curves do not become parallel.Īnswer: An intersection of a plane perpendicular to the bases of a double cone forms a hyperbola. Question 3: What is the difference between a parabola and a hyperbola?Īnswer: A parabola comprises of two arms of the curve which we also refer to as branches that become parallel to each other. Question 2: What is the focus of hyperbola?Īnswer: The foci of a hyperbola are the two fixed points which are situated inside each curve of a hyperbola which is useful in the curve’s formal definition.

Therefore, the equation of the required hyperbola is y 2/36 – x 2/108 = 1. Since ‘a’ cannot be negative, we take a = 6 and so b 2 = 36a/2 = (36 x 6)/2 = 108. Hence, from c 2 = a 2 + b 2, we have 12 2 = a 2 + 18a Question 1: Find the equation of the hyperbola where foci are (0, ☑2) and the length of the latus rectum is 36.Īnswer: The foci are (0, ☑2). The length of the latus rectum in hyperbola is 2b 2/a. Latus rectum of a hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose endpoints lie on the hyperbola. the transverse axis of x 2/9 – y 2/16 = 1 is along the x-axis and has length = 2a = 2 x √9 = 2 x 3 = 6. The denominator of the positive term gives the transverse axis. The foci always lie on the transverse axis.In simple words, if (m, n) is a point on the hyperbola, then (- m, n), (m, – n) and (- m, – n) also fall on it. A hyperbola is symmetric with respect to both the coordinate axes.
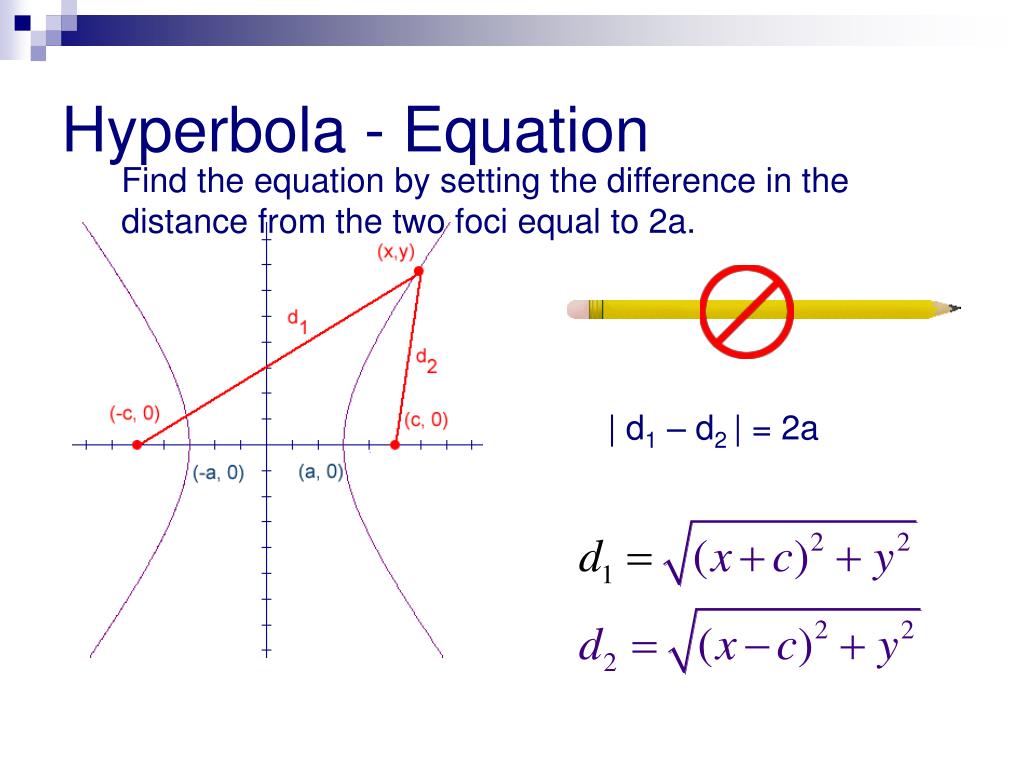
These two equations are known as the Standard Equations of Hyperbolas. Similarly, we can derive the equation of the hyperbola in Fig. Therefore, no portion of the curve lies between the lines x = + a and x = – a. Hence, it is evident that any point that satisfies the equation x 2/a 2 – y 2/b 2 = 1, lies on the hyperbola. Now, we take a point P(x, y) on the hyperbola such that, PF1 – PF2 = 2a Let the coordinates of F1 be (– c,0) and F2 be (c,0) shown in Fig. The line through O perpendicular to the x-axis be the y-axis. Let F1 and F2 be the foci and O be the mid-point of the line segment F1F2.Īlso, let O be the origin and the line through O through F2 be the positive x-axis and that through F1 as the negative x-axis. Of these, let’s derive the equation for the hyperbola shown in Fig.3 (a) with the foci on the x-axis. When the center of the hyperbola is at the origin and the foci are on the x-axis or y-axis, then the equation of the hyperbola is the simplest.


 0 kommentar(er)
0 kommentar(er)
